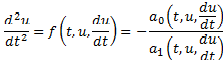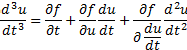Equação de Ergun

A perda de carga não ocorre apenas em tubulações e seus acessórios, mas também em equipamentos. A equação de Ergun tem a ver com o cálculo da fator de fricção em equipamentos baseado em leitos de partículas tais como reatores de leito fixo e colunas de destilação com recheio. Ela pode ser escrito da seguinte forma:

Neste expressão o número de Reynolds é calculado tendo por base o diâmetro das partículas como comprimento característico. Observe que a equação de Ergum tem duas parcelas . Eliminando a primeira parcela obtém-se a equação de Burk-Plummer que se aplica a valores de Reynolds maiores de 1000 onde as forças inerciais prevalecem

Eliminando a segunda parcela da equação de Ergun tem-se a equação de Kozeny-Carman

que se aplica a valores de Reynolds inferiores a um onde as forças viscosas prevalecem. O melhor mesmo é usar diretamente a equação de Ergun em qualquer situação.

Esta equação é devida ao engenheiro químico turco Sabri Ergun que a apresentou em 1952. Ergun nasceu em 1º de março de 1918 e morreu em 2006.

Chuva ácida

Por chuva ácida entende-se chuvas com pH abaixo do que se considera normal. Claro que a chuva não tem pH e que o pH da chuva é o pH da água da chuva. Chuvas normais tem pH em torno de 5,7 . A  leve acidez decorre do dióxido de carbono, que é considerado um componente permanente do ar e importante para os seres vivos. O dióxido de carbono reage com a água produzindo ácido carbônico. Abaixo deste pH a chuva é considerada ácida. No entanto, tem quem inclua no rol das chuvas ácidas a neve ácida, a neblina ácida e por ai vai. A culpa pela acidez excessiva cai principalmente nos óxidos de nitrogênio e enxofre, mais conhecidos como NOx e SOx.  A principal fonte natural deste óxido são as emissões vulcânicas e os relâmpagos e as principais fontes antrópicas são os combustíveis fosseis e as indústrias químicas.

Na foto a seguir obtida no site da National Geographic  mostra o efeito da chuva ácida sobre vegetação. Basicamente a chuva ácida queima as folhas.

Pratos versus recheio

Chega um ponto no projeto de uma coluna de fracionamento onde a escolha deve ser feita; pratos ou recheio? Trata-se de uma escolha baseada no bom senso.

1. O diâmetro da coluna é um dos critérios. Se a coluna tiver mais de um metro de diâmetro a escolha geralmente cai no prato. Se tiver menos de um metro de diâmetro, a escolha pende para o recheio.
2. A existência de sujeira na mistura processada é outro critério. É mais fácil limpar uma coluna de pratos do que uma coluna de recheio. Principalmente recheios de desenhos elaborados como, por exemplo, o tellerete.
3. Se a coluna processa mistura corrosiva, a escolha pende para recheio que pode ser de vidro, porcelana, teflon, etc. Também é mais fácil revestir a parede da coluna oca do que uma coluna cheia de pratos.
4. Se a mistura processada espuma, então a escolha deve pender para colunas recheadas. As colunas de pratos que se baseiam no borbulhamento do vapor no líquido em cada prato apenas agravam a formação de espuma.
5. Se o fracionamento deve ser feito sob vácuo, a perda de carga ao longo da coluna passa a ser importante. Neste caso as colunas recheadas são preferidas.
6. O peso de uma coluna de pratos é menor, isso facilita o dimensionamento do alicerce da coluna.
7. A altura das colunas recheadas é geralmente menor.

É possível numa mesma coluna uma seção ser de pratos e outra ser de recheio? A resposta é sim. Por exemplo, a seção de absorção (acima do ponto de alimentação) ser de recheio e a seção de esgotamento ( abaixo do ponto de alimentação) ser de pratos. Isso acontece dentro da lógica de seleção descrita acima aplicada a cada seção, mas o normal é não misturar prato e recheio na mesma coluna.

Escala Brix

É uma escala que mede a quantidade de sólidos solúveis numa solução usado nas usinas de açúcar e nas fábricas de alimentos. Foi criada por Adolfo Brix e deriva da escala Balling usada nos sacarímetros mais antigos. A escala Brix (ºBrix) mede aproximadamente a quantidade de sólidos solúveis em porcentagem ponderal. O sólido solúvel visado por esta escala é a sacarose, mas, se outros componentes sólidos estiverem presentes, a escala Brix dá a percentagem de sólidos solúveis totais em peso.

Adolf Ferdinand Brix nasceu em fevereiro de 1798 em Wiesel. A sua carreira como servidor publico se centrou em áreas centradas em engenharia civil, matemática e metrologia. Foi professor de matemática aplicada em Berlim de 1828 até 1850 em instituições precursoras da Universidade Técnica de Berlim, cidade onde morreu em 14 de fevereiro de 1870

Equação de Redlich-Kwong-Soave

O certo seria dizer equação de Redlich-Kwong modificada por Soave. A modificação foi necessária porque a equação de Redlich-Kwong não se saia bem na fase líquida. A forma da equação modificada é

A melhor forma de perceber as alterações é comparar as duas equações.

Diferença entre grau de avanço e conversão

O grau de avanço é uma propriedade da reação. Ele mede a extensão da reação. Aliás alguns preferem este nome. A conversão está relaciona a um componente chave, geralmente o componente medido ao longo da reação. É interessante que este componente seja o componente limitante cuja exaustão na mistura para a reação. Dada uma reação genérica

e considerando um componente limitante k, o grau de avanço é dado pela relação

Já a conversão é dada por

O valor grau de avanço independe do componente usado no cálculo. Já a conversão varia de componente para componente. A relação do conversão com o grau de avanço é

A conversão é um atributo de reagente e não deve ser aplicada a produtos sem uma longa meditação sobre as implicações. O sinal negativo decorre dos coeficientes estequiométrico dos reagentes serem negativos. Para tudo que foi dito acima ser válido a reação precisa ser isocórica.

Equação de Colebrook

Esta equação é usada no cálculo do fator de fricção de D’Arcy-Weisbach, k, em tubos no regime turbulento

Como não dá para explicitar k, o cálculo deve ser feito por via numérica. Outro parâmetro que aparece na equação acima é o diâmetro hidráulico, que corresponde ao quadruplo da área transversal dividido pelo perímetro molhado. O perímetro molhado é um parâmetro importante, ele considera apenas a parte do perímetro do cano molhada pelo fluido. Isso permite estender os cálculos para tubos que não estão completamente cheios e canais. Serve para calcular o número de Reynolds e o fator de fricção em tubo de qualquer seja a geometria do tubo.

Matemática em Java

Uma das grandes vantagens do Fortran, mencionada por todos os usuários, é que é uma linguagem voltada para formulas matemáticas.  Ela foi criada voltada para aplicativos voltados para ciência e engenharia. Ela é otimizada para resolver seguidamente formulas matemáticas, partindo de poucos dados para produzir poucos dados. Isso implica em que o processamento de dados deve ser o mais rápido possível.

Nos cálculos contábeis, o volume de dados alimentados descarregados é enorme. Neste caso, a entrada e saída de dados deve ser o mais rápido possível, mas o processamento nem tanto. A linguagem adequada neste caso é o Cobol.

O Java é uma linguagem voltada para redes. Então fica a questão: Como o Java processa dados? Muitos pensam que esta possibilidade nem existe nesta linguagem, mas existe.

As operações matemáticas básicas em Java são: soma (+), subtração (-), multiplicação (*), divisão (/) e modulo (%). O módulo é o resto da divisão de um número pelo outro.  Não há necessidade de maiores explicações. Praticamente todas as linguagens tem estes operadores. O Java tem vários operadores de atribuição. Aqui é bom explicar direito. São operadores de atribuição:

1. atribuição simples  x = y + z;
2. atribuição aditiva  x+=y     x = x + y;
3. atribuição subtrativa  x-=y    x = x – y
4. atribuição multiplicativa  x*=y     x = x*y
5. atribuição divisiva  x/=y     x = x/y;

No caso de incrementos, geralmente escrito desta forma

number = number + 1

em Java pode ser escrito da seguinte forma

number+=1

Pulando para as funções matemáticas do Java. Elas estão no pacote Math que deverá ser chamado. Então vamos lá

1. Raiz quadrada       Math.sqrt(x)  retorna a raiz quadrada de x;seno    Math.sin(x)      retorna o seno do angulo x em radianos;
2. cosseno Math.cos(x)   retorna o cosseno do angulo x em radianos;
3. tangente Math.tan (x)    retorna a tangente do angulo x em radianos;
4. arco do seno  Math.asin(x)    retorna o arco do seno x;
5. arco cosseno Math.acos(x)    retorna o arco do cosseno x;
6. logaritmo natural Math.log(x)  retorna o logaritmo natural de x;
7. potenciação  Math.pow(x,y)  retorna x elevado a y;
8. máximo   Math.max(x,y) retorna o maior valor x ou y;
9. mínimo   Math.min(x,y) retorna o menor valor x ou y;
10. numero randômico     Math.random(x)

Quem quiser mais fundo no Java deve procurar um bom livro.

Reações irreversíveis de primeira ordem

A forma geral das reações irreversíveis de primeira ordem é:

Nesta expressão os coeficientes estequiométricos dentro do somatório são positivos ou nulos. A expressão cinética da reação acima em fase líquida, desprezando a variação de volume é:

A condição inicial apropriada para este problema é:

Este problema de Cauchy pode ser resolvido por várias rotas. Como as variáveis estão separadas a equação doe ser escrita da seguinte forma:

Considerando a condição inicial e integrando resulta:

Outra forma de escrever este mesmo resultado é

Isso para o componente um, para os demais componentes o coeficiente estequiométrico deve ser considerado. Desta forma

A principal característica da reação reversível de primeira ordem, quando um dos componentes é acompanhado versus tempo, é a linearidade entre concentração e tempo num gráfico semilog

EDO–Problemas de segunda ordem

EDO de segunda ordem

Denomina-se equação diferencial ordinária de segunda ordem a toda equação que relacione uma variável independente, , uma função desconhecida desta variável, , e as derivadas de primeira e segunda ordens desta função. A forma geral destas equações é

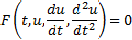
Neste ponto vale salientar que a variável independente tanto pode ser o tempo ou uma variável espacial como uma distância, . A natureza do problema determina qual deve ser escolhida.

Para determinar o grau desta equação, basta escreve-la como um polinômio na derivada de segunda ordem. O grau do polinômio será o grau da equação diferencial. A forma geral de uma equação do terceiro grau é

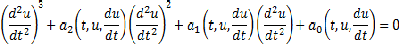
Deixando as equações de graus superiores para outro momento e concentrando a nossa atenção nas equações de primeiro grau, então, se a derivada de segunda ordem puder ser explicitada, nem sempre isso é possível, a equação poderá ser escrita da seguinte forma:

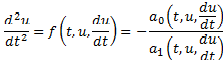
Esta é a forma mais comum de apresentação das equações diferenciais de segunda ordem na engenharia química. As equações que se reduzem a esta forma geral são de segunda ordem e primeiro grau.

Problema de valor inicial

Esta equação pode gerar dois tipos de problemas: um conhecido como problema de valor inicial ou problema de Cauchy e outro conhecido como problema de valor de contorno.

O problema de Cauchy, em sua forma mais comum consiste em fixar os valores da função desconhecida e da sua derivada de primeira ordem no instante inicial, e calcular o valor da derivada de segunda ordem usando a equação diferencial. Este problema pode ser escrito da seguinte forma

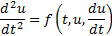
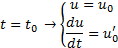
Conhecendo-se a derivada de segunda ordem no ponto inicial, a derivada de terceira ordem é dada por

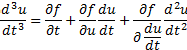
e assim sucessiva mente para obter todas as derivadas de ordens superiores. O conhecimento das derivadas permite o desenvolvimento em série de Taylor da solução. É claro que questões sobre a convergência da série e sobre a existência e unicidade de solução podem aparecer para a delícia dos matemáticos.

Problemas de valor de contorno.

Nos problemas de valor inicial, a variável independente é geralmente o tempo. Nos problemas de vapor de contorno, a variável independente é uma distância espacial. Por isso, t será substituído por x. No problema de valor de contorno, a função desconhecida é especificada em dois pontos. Assim,

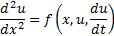
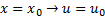
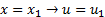
Quem for mais atento com certeza percebeu estar diante se um sistema de duas equações e duas incógnitas . As duas incógnitas são exatamente as derivadas da função desconhecida. Se é possível resolver é outra questão. Fica para depois.

Fator de caracterização K de Watson

O fator de caracterização de Watson está ligado  a aromaticidade e a parafinicidade do petróleo ou fração. Ele é calculado pela fórmula:

Por extenso, é a razão  entre a raiz cúbica do ponto de ebulição médio (MABP) em ºR, e a densidade específica a 15ºC  (60ºF) do petróleo. Este fator varia de 10 a 15. O valor 10 corresponde a alta aromaticidade e o valor 15 a alta parafinicidade.Este fator de caracterização pode servir para outras coisas como determinar o índice de viscosidade, o peso molecular, a temperatura crítica, o ponto de anilina, etc. Vale tanto para substâncias puras como para misturas já que segue a regra de mistura. O fator de caracterização do propano é 14,7, do tolueno, 10.1 e do ciclopentano, 11,2. O fator de caracterização de Watson segue a regra de mistura o que facilita os cálculos. Assim

Solubilidade de ácidos, bases, sais e óxidos em água

É sempre bom saber .

• Qualquer que seja o ânion, os sais dos metais alcalinos e de amônia são solúveis;
• Qualquer que seja o ânion, os ácidos correspondentes são solúveis;
• Todos os nitratos e acetatos são solúveis;
• Os halogenetos (cloreto, iodeto e brometo) são solúveis excetos os de prata, chumbo e mercúrio (I);
• Os sulfatos de cálcio, bário, estrôncio, prata, chumbo e radio são insolúveis e todos os demais solúveis;
• Todos os carbonatos, sulfitos e fosfatos são insolúveis exceto os de metais alcalinos, de amônia;
• Todos os hidróxidos são insolúveis exceto os de metais alcalinos, amônia e bário;
• Os sulfetos dos metais alcalinos, alcalinos terrosos e amônia são solúveis e todos os demais insolúveis e
• Todos os óxidos são insolúveis exceto os de metais alcalinos, cálcio e bário.